指数部
| 日本語 | 浮動小数点の指数の部分 |
| 英語 | exponent bits |
| ふりがな | しすうぶ |
| フリガナ | シスウブ |
浮動小数点の中の「2の累乗」の部分。
double型の場合、全64ビットの内、1ビット目~11ビット目(左端のビットを0ビット目とした場合)が指数部となる。
float型の場合、全32ビットの内、1ビット目~8ビット目(左端のビットを0ビット目とした場合)が指数部となる。
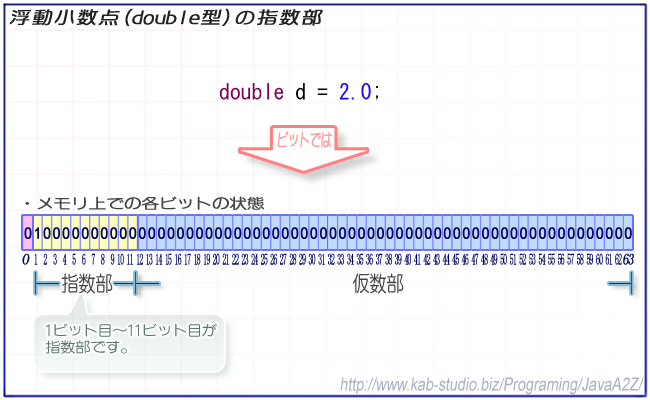
以下、double型における、浮動小数点の指数部について説明する。
指数部には「2の累乗」が整数値として格納されている。-1023~1023の値を、整数型と似たような形式で格納する。つまり指数部は「2の-1023乗」~「2の1023乗」までの値を表現できる。
つまり指数部は、「2の累乗」という非常におおざっぱな値しか表現しない。指数部はビット的に1増えただけで2倍されることになり、2、4、8、16...という飛び飛びの値を表現することになる。
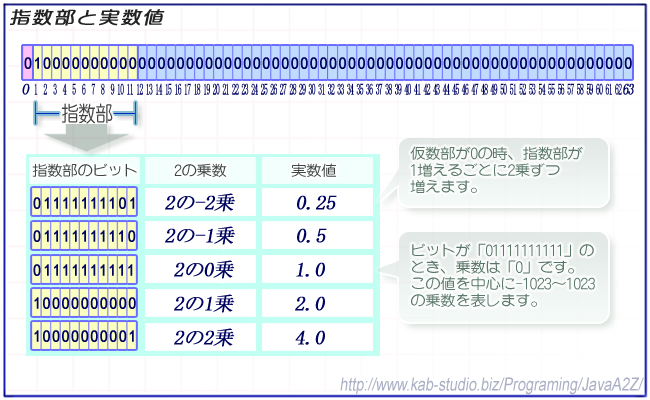
この飛び飛びの値の「間の値」を作り出すために「仮数部」が存在する。指数部と仮数部を掛けた値が実際の値となる。
指数部に格納される「2の累乗」は、2進数での「小数点の位置」を意味する。
これは、10進数において「10の累乗」が小数点の位置を示すのと同じである。これが、「浮動小数点」という名称の由来である。
double型の場合、全64ビットの内、1ビット目~11ビット目(左端のビットを0ビット目とした場合)が指数部となる。
float型の場合、全32ビットの内、1ビット目~8ビット目(左端のビットを0ビット目とした場合)が指数部となる。

以下、double型における、浮動小数点の指数部について説明する。
指数部には「2の累乗」が整数値として格納されている。-1023~1023の値を、整数型と似たような形式で格納する。つまり指数部は「2の-1023乗」~「2の1023乗」までの値を表現できる。
つまり指数部は、「2の累乗」という非常におおざっぱな値しか表現しない。指数部はビット的に1増えただけで2倍されることになり、2、4、8、16...という飛び飛びの値を表現することになる。

この飛び飛びの値の「間の値」を作り出すために「仮数部」が存在する。指数部と仮数部を掛けた値が実際の値となる。
指数部に格納される「2の累乗」は、2進数での「小数点の位置」を意味する。
これは、10進数において「10の累乗」が小数点の位置を示すのと同じである。これが、「浮動小数点」という名称の由来である。
// Sample.java
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// この「2.0」という値を、指数部のビット「10000000000」
// で表現します。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// double型の1ビット目~11ビット目は指数部が格納されます。
// これは「2の累乗」を表します。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// 01111111100 : 0.125 : 2の-3乗 :
// 01111111101 : 0.25 : 2の-2乗
// 01111111110 : 0.5 : 2の-1乗
// 01111111111 : 1.0 : 2の 0乗 ↓指数部の値を2進数で表現した場合。
// 10000000000 : 2.0 : 2の 1乗 : 0001
// 10000000001 : 4.0 : 2の 2乗 : 0010
// 10000000010 : 8.0 : 2の 3乗 : 0100
// 10000000011 : 16.0 : 2の 4乗 : 1000
// このように、ビットは「累乗」を表しています。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// つまり、マイナスの場合でも2の補数を使いません。
// 上記の「指数部の値を2進数で表現した場合」にあるように、
// 2進数では乗数が1増えれば桁が1増えます。
// これが「小数点が動く」ということです。
// 指数部では、おおざっぱな値しか取れません。
outputDoubleBit( 512.0 );
outputDoubleBit( 1024.0 );
// 0 10000001000 0000000000000000000000000000000000000000000000000000
// 0 10000001001 0000000000000000000000000000000000000000000000000000
// このように、指数部のビット的には1しか増えていませんが、
// 512から1024と大きく数が増えています。
// この512と1024の値を埋めるのが、仮数部ということです。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// この「2.0」という値を、指数部のビット「10000000000」
// で表現します。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// double型の1ビット目~11ビット目は指数部が格納されます。
// これは「2の累乗」を表します。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// 01111111100 : 0.125 : 2の-3乗 :
// 01111111101 : 0.25 : 2の-2乗
// 01111111110 : 0.5 : 2の-1乗
// 01111111111 : 1.0 : 2の 0乗 ↓指数部の値を2進数で表現した場合。
// 10000000000 : 2.0 : 2の 1乗 : 0001
// 10000000001 : 4.0 : 2の 2乗 : 0010
// 10000000010 : 8.0 : 2の 3乗 : 0100
// 10000000011 : 16.0 : 2の 4乗 : 1000
// このように、ビットは「累乗」を表しています。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// つまり、マイナスの場合でも2の補数を使いません。
// 上記の「指数部の値を2進数で表現した場合」にあるように、
// 2進数では乗数が1増えれば桁が1増えます。
// これが「小数点が動く」ということです。
// 指数部では、おおざっぱな値しか取れません。
outputDoubleBit( 512.0 );
outputDoubleBit( 1024.0 );
// 0 10000001000 0000000000000000000000000000000000000000000000000000
// 0 10000001001 0000000000000000000000000000000000000000000000000000
// このように、指数部のビット的には1しか増えていませんが、
// 512から1024と大きく数が増えています。
// この512と1024の値を埋めるのが、仮数部ということです。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}
// Sample.java
public class Sample
{
public static void main( String[] args )
{
// 浮動小数点で一番「普通」の値は「2.0」です。
// この「2.0」という値を、指数部のビット「10000000000」
// で表現します。
outputDoubleBit( 2.0 );
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// ←指数部 → ←仮数部 →
// double型の1ビット目~11ビット目は指数部が格納されます。
// これは「2の累乗」を表します。
outputDoubleBit( 0.125 );
outputDoubleBit( 0.25 );
outputDoubleBit( 0.5 );
outputDoubleBit( 1.0 );
outputDoubleBit( 2.0 );
outputDoubleBit( 4.0 );
outputDoubleBit( 8.0 );
outputDoubleBit( 16.0 );
// 0 01111111100 0000000000000000000000000000000000000000000000000000
// 0 01111111101 0000000000000000000000000000000000000000000000000000
// 0 01111111110 0000000000000000000000000000000000000000000000000000
// 0 01111111111 0000000000000000000000000000000000000000000000000000
// 0 10000000000 0000000000000000000000000000000000000000000000000000
// 0 10000000001 0000000000000000000000000000000000000000000000000000
// 0 10000000010 0000000000000000000000000000000000000000000000000000
// 0 10000000011 0000000000000000000000000000000000000000000000000000
// 指数のビットは、整数とほぼ同じです。
// 01111111100 : 0.125 : 2の-3乗 :
// 01111111101 : 0.25 : 2の-2乗
// 01111111110 : 0.5 : 2の-1乗
// 01111111111 : 1.0 : 2の 0乗 ↓指数部の値を2進数で表現した場合。
// 10000000000 : 2.0 : 2の 1乗 : 0001
// 10000000001 : 4.0 : 2の 2乗 : 0010
// 10000000010 : 8.0 : 2の 3乗 : 0100
// 10000000011 : 16.0 : 2の 4乗 : 1000
// このように、ビットは「累乗」を表しています。
// ただし、2の-1023乗の時に00000000000、
// 2の1023乗の時に11111111111となります。
// つまり、マイナスの場合でも2の補数を使いません。
// 上記の「指数部の値を2進数で表現した場合」にあるように、
// 2進数では乗数が1増えれば桁が1増えます。
// これが「小数点が動く」ということです。
// 指数部では、おおざっぱな値しか取れません。
outputDoubleBit( 512.0 );
outputDoubleBit( 1024.0 );
// 0 10000001000 0000000000000000000000000000000000000000000000000000
// 0 10000001001 0000000000000000000000000000000000000000000000000000
// このように、指数部のビット的には1しか増えていませんが、
// 512から1024と大きく数が増えています。
// この512と1024の値を埋めるのが、仮数部ということです。
}
/**
* double型変数をビット形式で出力します。
*/
private static void outputDoubleBit( double d )
{
// double型変数をビット形式で文字列化します。
String source = Long.toBinaryString( Double.doubleToLongBits( d ) );
// 左0埋めします。
StringBuffer strbuf = new StringBuffer();
for( int iF1 = source.length(); iF1 < 64; ++iF1 )
{
strbuf.append( "0" );
}
strbuf.append( source );
// 符号、仮数部、指数部の間にスペースを入れます。
strbuf.insert( 12, " " );
strbuf.insert( 1, " " );
System.out.println( strbuf.toString() );
}
}






