いよいよＣｏｄｉａｎでもポインタについての解説をしようと思います（って言っても現時点で９割方書き終えてますが（汗））。
　ポインタはＣ言語の根幹と言っても過言ではないアーキテクチャーです。ですから、すでにありとあらゆる本で解説され、その中にはとうてい追い抜くことのできないほどの良書も数多く存在します。また、ポインタを利用したアルゴリズムもこれまた無数にあり、これをすべて解説するのはとうてい不可能です。
　
　というわけで、他のページと同じようにＣｏｄｉａｎらしく、概念的な解説を中心に行いたいと思います。また、Ｃｏｄｉａｎがそうであるように、このポインタ講座もＶｉｓｕａｌ　Ｃ＋＋のユーザーが読んでいるものとして書いていきます。これはよーするに「他とは違う」ということです。かなり異色に見えても大目に見てください（汗）（でも明らかな間違いがあったら教えてくださいね）。
　
　さて、その第１回目は「コンピューターはどんなふうなしくみで動いているのか」ということを見ていこうと思います。ま、最初はプログラムそのものが出てこないので、気楽に読んでみてください。
　では、はじまりはじまり。

もしも「もしも」があったなら
　世の中は「もしも」であふれています。たとえば「もし大根が１００円なら買うけど、２００円なら買わない」とか、「もしこのスイッチを入れたのなら灯りは点くけど、入れなかったら暗いまま」とか、「もし秒速１０メートルで飛べれば宇宙へ行けるが、８メートルだったら地球から出られない」とか、「もし１に１を足せば２だけど、１０を足せば１１になる」のように、ありとあらゆるところに「もしも」は存在します。
　「もしも」があるのは、そこに「未来」があるからです。過去はどーやったって変えられません。過去には「もしも」がないのです。人間は幸せに生きるために、より良い過去を作ろうとします。そのより良い過去を作るために、「もしも」が必要になってきます。
　
　「もしも」は、未来を予測して過去を選択するためのものです。無駄な出費を防ぐためにできるだけ安い大根を買おうとしたり、電気を節約するために必要なときだけ灯りを点けたりすることが生活に非常に大きな意味を持ってきます。逆に、何がどうあろうと秒速８メートルでロケットを飛ばしているような頑固さを持っていたらいつまでも宇宙には飛び出せません。
　現実は小説のように決まり切った世界ではなく、少なくとも人間の目から見れば、この世界には十分な自由度があるように感じられます。アドベンチャーゲームのように、現実の世界でも最良の手を打つことが必要で、そのための手段が「もしも」なのです。

「もしも」の自動化
　ところが、「もしも」には必要なものがあります。それは「思考実験」です。
　たとえば「１＋１は２だけど、１＋１０なら１１」という「もしも」は「計算」という「思考実験」をしなければなりません。このように簡単で、結構面倒で、しかも誰だってできる「もしも」もあれば、「もし私が告白したら、彼はなんて言うだろう」みたいなまず答の出ない思考実験もあります。
　この「簡単に答の出るもしも」と「答のなかなか出ないもしも」では、おそらく誰もが「答の出ない」方に時間を費やしたい、「簡単に出るもしも」はあまりしたくないと考えるでしょう。この「簡単なもしも」を自動化できたら、「答の出ないもしも」により時間を割くことができます。
　
　実は、「簡単なもしも」の自動化は結構簡単に実現できます。たとえば、天秤。ふたつの物を天秤に掛けたとき、もし左の物の方が重ければ左に傾き、右の方が重ければ右の方に傾きます。こういった「科学法則」は、「もしも」のいくつかを実験という形で解決してくれます。
　でも天秤では用途が狭すぎます。これまで見てきた「簡単なもしも」をそんなに複雑にならずに解決できないでしょうか。というわけで出てきたのが「ＮＡＮＤ」です。

ＮＡＮＤ（なんど）
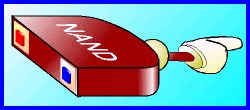　天秤のような機能を持っていて、しかもいろんなことに使える機械はないだろうか、というわけで出てきたのがＮＡＮＤ（なんど）と呼ばれる機械（っていうか機構）です。
　ＮＡＮＤにはふたつのボタンとひとつの指が着いています。指は何もしてない状態で出ています。また、一方のボタンだけを押しても出たままです。両方のボタンを同時に押したときのみ、指が引っ込みます。これを表にすると、次のようになります。

　「ボタン１を押していて、かつ（ＡＮＤ）ボタン２を押しているときだけ、出ていない（ＮＯＴ）」から、ＮＡＮＤというわけです。

これが何に使えるの？
　まずものすごーく単純な例として、「太る」というものを考えてみましょう。ボタン１に「階段を上る」を、ボタン２に「早歩きをする」を割り当ててみましょう。どちらも運動にはなりますが、もし元々太っているのなら、やはり両方を試した方がやせるでしょう。
　この割り当てを変えて、ボタン１を「運動する」に、ボタン２を「よく食べる」にするとします。が、これだと矛盾してしまいます。矛盾しないようにするにはボタン２を「あまり食べない」とするのが一番ですが、「私はよく食べたときにボタンを押したい！」というユーザーの気持ちに応えることも大事です。
　
　こういう場合には、ボタン２の前にもうひとつＮＡＮＤを用意します。このとき、ボタンを押したときにはふたつのボタン両方とも押すようにします。
　ＮＡＮＤには「入力をひとつとするとただの否定（ＮＯＴ）になる」という性質があります。上の表で確かめてみてください。この性質を利用してボタン２の前に入れると、「よく食べた」ときにボタン２を押さず、「よく食べなかった」ときにボタン２を押すことになります。これで、ちゃんとした結果が出るようになりました。
　
　ＮＡＮＤのこの性質を利用すると、上の表の逆の結果、つまり「両方押しているときだけ指が出る」というもの（これはＡＮＤですね）も簡単にできます。ＮＡＮＤの指の先にもうひとつＮＡＮＤをおけばいいわけです。
　そのほか、実はＮＡＮＤだけを組み合わせれば、ありとあらゆる条件を作ることができるようになります。そうすると……。

メモリをＮＡＮＤで
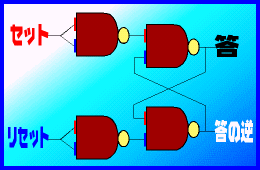　このＮＡＮＤを４つ使って右のようなシステムを組んでみましょう。指だと届かない部分は、カメラのシャッターを押す「レリース」のようなものを使えば実現できます。で、これが何に使えるかというと、このシステムで「データを保存できる」のです。
　
　「セット」のスイッチを「押す」、かつ「リセット」を「押さないと」にすると、「Ｃ」の上側のボタンは「押さない」になります。ＮＡＮＤは「押さない」がひとつでもあれば「指を出す」ので、「答」の部分は「指を出す」になります。
　さらに、この指はレリースを通して「Ｄ」の上のボタンを「押し」ます。「リセット」は「押さない」になっているので、「Ｄ」の下のボタンも「押す」になります。結果、Ｄは「押さない」を出力します。これが「答の逆」の結果になります。
　
　さて、この状態で「セット」のボタンを離してみましょう。「Ｃ」の上ボタンは「押す」になります。が、実はＤの出力「押さない」が「Ｃ」の下ボタンに入っています。ということは「Ｃ」は指を「出す」という出力、つまり先ほどと同じ結果になります。リセットの方は離したままなので、「答」は「指を出す」のままということになります。
　
　今度は「リセット」のボタンを「押し」てみましょう。これは先ほどの「セット」を上下逆にして見ていけばいいので、結果、「答の逆」は「指を出す」、「答」は「指を出さない」になります。
　さらに同じように「リセット」ボタンを離せば、この状態が維持されます。
　
　これをまとめると、次のようになります。

　と、このシステムは「セットを押せば指が出て、リセットを押せば指が引っ込む」と機能します。特に注目して欲しいのは、「両方離せば前の状態を維持する」という点です。このおかげで、結果に対して「入力し続ける」ということをしなくてすみます。
　
　もうおわかりでしょうが、これが「メモリ」の基本原理です。このシステムひとつで「ふたつの状態」を表すことができます。このシステムをいっぱい使えばそれだけ多くの状態を表すことができます。このメモリを使ってどうやって数字や文字を表すかという部分は、次回の「変数のなかみ」で紹介します。

足し算をＮＡＮＤで
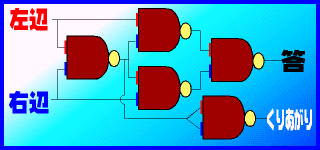　もうひとつ、今度は計算をしてみましょう。まず、「１＋１」を計算するシステムを組んでみます。足し算をＮＡＮＤで実現する場合には、右図のように組み合わせます。ボタンを押したときに「１」、押さなかったら「０」とすると、「どっちかのボタンを押したとき」つまり「１＋０」か「０＋１」の時に「指が出る」、それ以外の場合には「指が出ない」というものになります。
　「ええっ？　それじゃ足し算にならんやん！」と思われることでしょう。でもよく見てください。もうひとつ出力があるでしょう。これはくりあがりです。これが出てるときには「繰り上がって、次に加える」ということにします。で、２より大きい数はこのシステムを使って、また同じようにして足していきます。これを何度も何度も繰り返して、足し算をしていくわけです。
　
　もちろん、実際のコンピューターに使われているものは、もっと最適化されていますし、少数なども扱えるようになっています。
　これと同じようにして引き算（これは次回説明する「補数」というものを使用します）、かけ算（足し算の応用でできます）、わり算（これも引き算の応用でできます）も、ＮＡＮＤを組み合わせることで可能になるというわけです。
　これが、コンピューターの基本的な仕組みです。

ＮＡＮＤの作り方
　さて、問題は「ＮＡＮＤをどのように作るか」という問題です。ＮＡＮＤそのものは、「バネ」や「クランク」を組み合わせることで機械的に作れてしまいます。実際、コンピューターの基礎的な概念――２進数を用いた計算方法など――は１７世紀頃には考え出されていて、１８〜１９世紀にはこういった「機械式コンピューター」が存在しました。
　ですが、機械を組み合わせたものではあまりにもサイズが大きくなってしまい、またメンテナンスが大変になります。「力」が加わる関係で、精密に作らないと動かないという問題もありました。
　もっと小型で確実なものを。そして、そのころ実用化された「電気」を用いて作れたら……。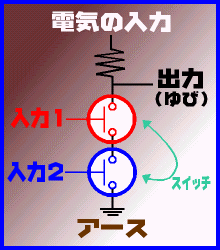
　
　というわけで考え出されたのが右のような回路です。「電気の入力」は文字通り電気が送られています。「出力」には、「オン」の時に電気が流れ、「オフ」の時には電気が止まります。「アース」は電気の逃げ道で、電気の通り道にアースがあるとすべてアースへと流れてしまいます。「スイッチ」はそのままスイッチ。スイッチがオンなら電気が流れ、オフなら流れません。
　右の図はそのままＮＡＮＤを表しています。スイッチは「入力」です。スイッチがひとつでもオフなら、アースへのコードが途切れるので、電気は出力へと流れていきます。
　スイッチをふたつとも「オン」にすると、アースへの道が開きます。アースと出力両方あった場合、電気はすべてアースへと流れてしまいます。というわけで、結果「出力」には電気が流れなくなってしまいます。このようにして、ＮＡＮＤを実現しているのです。
　
　でもちょっと変でしょう。そう、「スイッチ」です。この図ではスイッチは押さなければなりません。ＮＡＮＤをくっつけ合わせる場合には、これも電気でオンオフできなければならなくなってしまいます。この部分を解決したのが「半導体」です（真空管は飛ばしますね）。

半導体の登場
　物質にはみっつのタイプがあります。導体、絶縁体、半導体です。
　「導体」は「電気を通すもの」です。鉄や銅といった金属が有名でしょう。
　逆に「絶縁体」は「電気を通さないもの」です。これはゴムやプラスチックが有名でしょう。
　
　「半導体」は、このふたつの中間です。普段は電気を通しませんが、周りから「エネルギー」を受けると電気が通りやすくなります。「エネルギー」は基本的にたいがいのものが使えます。そう、このエネルギーに電気が使えるのです。
　半導体に電気を加えると、電気が通りやすくなります。これこそ「電気を使ったスイッチ」です。このスイッチは電気を使え、小型化でき、確実性も高いとメリットが非常に多い物質です。実際には、純度の高い半導体を生成することが難しかったのですが、２０世紀に入ってその技術が確立され、今に至るというわけです。
　ちなみにデメリットのひとつとして「熱に弱い」という面もあります。熱もエネルギーのひとつなので、熱を与えると「スイッチ」が勝手に入ってしまい、熱暴走してしまうというわけです。冷却は十分に行うようにしましょう。

と、言うわけで
　というわけで、コンピューターがどんな感じなのか、簡単に見てきました。今回だけだと単なる「雑学コーナー」ですが、次回の「変数のなかみ」を読むときには非常に役立つ内容だと思います。
　ポインタ編はまだまだ続きます。ま、のんびり読み進めていってください。